
Le basi teoriche della digitalizzazione applicata alle immagini
Affinchè una immagine possa essere trattata digitalmente attraverso un computer essa deve essere disponibile in forma digitale. Il processo per ottenere una immagine digitale a partire dal mondo analogico passa attraverso due fasi principali che stanno alla base di tutto il mondo digitale: il campionamento e la quantizzazione. L’immagine digitale viene ottenuta campionando una immagine a toni continui attraverso una “griglia discreta” e quantizzando poi i valori campionati con un numero finito di bit.
Il Campionamento
Le basi teoriche sono costituite dal teorema del campionamento, in questo caso applicato a segnali 2D. Il teorema si applica a tutti i segnali 2D a banda limitata: un segnale (una immagine) 2D si dice a banda limitata se la sua trasformata di Fourier è nulla al di fuori di una regione limitata nello spazio delle frequenze, ovvero se il suo spettro frequenziale è limitato. Sotto queste ipotesi il teorema assicura che il segnale analogico (la nostra immagine) potrà essere ricostruito attraverso un filtro passa-basso dai suoi campioni, ammesso che non vi siano sovrapposizioni tra le sue componenti spettrali (fenomeno indesiderato noto con il nome di Aliasing). Il teorema dimostra che questo sarà possibile solo se il segnale 2D originale verrà campionato ad una frequenza almeno pari al doppio della massima frequenza presente nello spettro del segnale analogico, sia per l’asse x che per l’asse y. Questa frequenza minima di campionamento è nota con il nome di frequenza di Nyquist. Se un segnale viene sottocampionato, ovvero campionato ad una frequenza inferiore alla frequenza di Nyquist, avremo il fenomeno dell’alias. L’effetto dell’alias sarà quello di avere che le alte frequenze nel segnale originale verranno mappate come basse frequenze del segnale campionato.
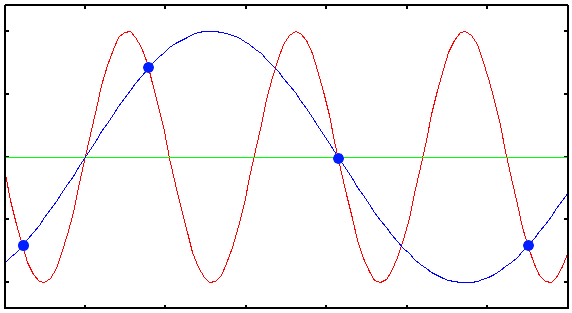
Per evitare l’alias, il segnale originale deve essere filtrato prima del campionamento: più precisamente il filtro dovà eliminare tutte le frequenze al di sopra della metà della frequenza di Nyquist. Questo filtro viene chiamato per questo motivo filtro anti-alias. Il filtro in pratica deve eliminare dal nostro segnale sorgente tutte le frequenze che andrebbero al di là della frequenza di campionamento “che possiamo permetterci”. Da notare che il filtraggio anti-alias deve avvenire necessariamente prima del campionamento. Una volta che il segnale sia stato sottocampionato e quindi dopo la comparsa dell’alias non vi è più modo di eliminare l’effetto indesiderato.

Il fenomeno dell’alias è particolarmente presente nelle fotocamere digitali che utilizzano i sensori CCD: questo di solito è dovuto al fatto che le ottiche, se di buona qualità, sono in grado di riprodurre accuratamente frequenze ben al di sopra della metà della frequenza di Nyquist (quest’ultima determinata in modo fisso dalla risoluzione del gruppo di sensori CCD). Un filtro anti-alias dovrà quindi essere presente tra il gruppo ottico e i sensori.
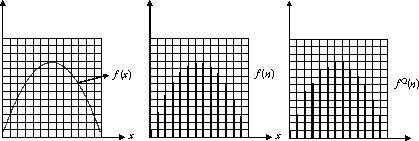
Quantizzazione dell’immagine (scalare e vettoriale)
Una volta ache il segnale è stato campionato, deve essere quantizzata l’ampiezza dei valori campionati. Un quantizzatore in sostanza “mappa” un range di valori di ingresso in un unico valore di uscita. Questo deve avvenire in quanto, in un segnale analogico, il range di valori tra due estremi è infinito mentre nel mondo digitale solo un certo numero di valori potrà essere rappresentato. La quantizzazione può essere di tipo scalare (SQ) oppure vettoriale (VQ). Nella SQ, ciascun campione viene quantizzato singolarmente, mentre nella VQ vengono quantizzati congiuntamente blocchi di campioni. A sua volta i modi secondo cui il quantizzatore può operare sono diversi, i più comuni sono la quantizzazione uniforme e la quantizzazione a minimo errore quadratico medio.
SQ e quantizzazione uniforme
Nel caso di quantizzazione uniforme, il gradino d di quantizzazione è uniforme cioè sempre della stessa ampiezza. Questo gradino (detto anche passo di quantizzazione) viene determinato a partire dalla massima dinamica del segnale di ingresso e dal numero di bit che abbiamo a disposizione. Detto R=[xmax,xmin] il range dinamico del segnale di ingresso e detto n il numero di bit a disposizione avremo: d=R/2n. Per chiarire con un semplice esempio: supponiamo che un panorama che vogliamo fotografare abbia livelli di luce compresi tra 0 e 128 (in una certa scala immaginaria) e supponiamo che il nostro quantizzatore abbia 8 bit: il passo di quantizzazione sarà d=(128-0)/28= 0,5. Questo significa che il segnale quantizzato, invece degli infiniti valori di luminosità compresi ad esempio tra 100 e 100,5 che erano presenti nel segnale analogico, avrà solo 2 valori e precisamente 100 e 100,5. Ovviamente agendo in questo modo la quantizzazione introduce un errore, detto errore di quantizzazione.
Errore di quantizzazione nel caso di quantizzazione uniforme
Correlato all’errore di quantizzazione è il concetto di rapporto segnale/rumore di quantizzazione (SQNR). Esso rappresenta un indice di qualità relativamente alla quantizzazione e quanto più elevato tanto più basso sarà l’errore di quantizzazione che (inevitabilmente) si è ottenuto quantizzando il segnale campionato. Tralasciando in questa sede i dettagli matematici è possibile dimostrare che tale rapporto aumenta di 6 dB per ogni bit aggiuntivo a disposizione della quantizzazione. Questo del resto era abbastanza intuitivo: ovvero aumentando il numero di bit a disposizione per la quantizzazione, il passo d diventa più piccolo ed il segnale analogico può venire quantizzato più “finemente”.
Le immagini digitali sono ottenute o attraverso acquisizione da scanner di una immagine a toni continui o attraverso l’acquisizione diretta ad esempio attraverso una fotocamera digitale. Nelle fotocamere digitali, ad esempio, il campionamento viene effettuato da una griglia di sensori CCD. Per ogni pixel del sensore, un fotodiodo converte i fotoni incidenti (luminosità) in elettroni che rappresentano poi l’intensità del pixel. In molti dispositivi digitali è consuetudine quantizzare il valore dell’intensità del pixel con 8 bit (quindi 256 livelli) poiché si ritiene che l’occhio umano non sia in grado di distinguere più di 100-200 livelli di luminosità. La quantizzazione a 12 o anche a 14 bit non è tuttavia infrequente in ambito medicale o altri settori.
E’ noto altresì che la quantizzazione uniforme della intensità dei pixel ( che dipende in sostanza dal conteggio dei fotoni incidenti) crea di solito artefatti visivi, questo perché differenze uguali nel conteggio dei fotoni non corrisponde ad uguali differenze nella percezione della luminosità. Ad esempio una piccola differenza nel numero dei fotoni a basse intensità sarà ben visibile all’occhio mentre anche una grande differenza ad alte intensità può risultare invisibile. Di conseguenza in molti sistemi la quantizzazione viene effettuata nel dominio della percezione visiva piuttosto che in quello della intensità luminosa. E’ stato teorizzato che il sistema visivo umano risponda in modo circa proporzionale alla percentuale di variazione nell’intensità, ovvero si è suggerita una relazione circa logaritmica tra l’intensità della luce e la nostra percezione di luminosità.
La quantizzazione su base percettiva si fonda su due metodologie: nella prima tecnica, l’intensità del pixel viene prima quantizzata su un gran numero di livelli usando 10-14 bit; poi questo valore viene riquantizzato a 8 bit attraverso una tabella non lineare (digital lookup table=LUT) che simula una trasformazione logaritmica. Ad esempio uno scanner ad alta risoluzione misura (cioè quantizza) i valori di intensità del pixel a 13 bit ed usa poi una LUT per convertirli a 8 bit. Nella seconda tecnica, il segnale analogico viene prima convertito nel dominio della percezione attraverso un dispositivo analogico non lineare (ad esempio un amplificatore logaritmico) e l’uscita viene poi successivamente quantizzata a 8 bit. Questo secondo approccio tuttavia sebbene meno costoso (necessita di una sola quantizzazione) è anche meno accurato.
